Much of the financial management industry operates on dogma. And much of that dogma is founded on sound finance theory. The past 50 years have seen some brilliant advances in finance theory and in our understanding of the proper functioning of the capital markets, but what is brilliant can be blinding.
Is our industry so eager to accept shortcuts, by accepting finance theory as fact, that it loses sight of its mission: to identify opportunities that can help our clients to achieve their goals?
* Modern portfolio theory, as developed by Harry Markowitz 50 years ago, is sound. The resulting optimization methods will maximize return at any given level of risk or minimize risk at any given level of return . . . if the assumptions about return, risk and covariance are correct forecasts for the future.
* The capital asset pricing model (CAPM) market line defines the correct expectational return of assets, based on a nondiversifiable beta, relative to a market portfolio . . . as long as borrowing and lending rates are the same, investors are willing to leverage, the risk premium is positive, investors are rational, taxes don’t exist and so forth.
* Fischer Black and Myron Scholes demonstrate that options can be valued with precision . . . if return distributions are lognormal, risk is known and there is a well-defined risk-free rate.
* Merton Miller and Franco Modigliani prove that capitalization structure and dividend policy don’t matter . . . if there are no taxes, investors are rational and managers operate in the sole best interests of the shareholder. The Miller-Modigliani proof has been construed intertemporally to imply that if the market retains more earnings and pays lower dividends, subsequent earnings growth will offset the lost dividend income.
| Arithmetic of long-term returns |
* Daniel Kahneman and Amos Tversky’s pioneering work in behavioral finance shows how human psychology can lead to market inefficiencies and mispricing opportunities, as investors’ time horizon is foreshortened by regret, as holdings are divided into segments that impede the quest for optimal portfolios . . . but this work tells us little about how to identify those opportunities.
* Richard Roll and Steven Ross, with their development of arbitrage pricing theory (APT), and later Eugene Fama and Kenneth French, with their work in identifying factors of return, take us beyond the single-factor CAPM into a world of more richly defined risk measurement. These multifactor pricing models also point us toward return opportunities, albeit with the caveat of well-defined additional risks . . . if we can depend on many of the same assumptions as the CAPM.
* John Cox, Jonathan Ingersoll and Steve Ross developed the bond world’s equivalent of the CAPM, a model that describes the entire term structure of interest rates as a function of the current short rate and three term structure constants . . . if there is a fixed “normal” short rate that is the anchor for mean reversion, if volatility is a function of short rates and if no factors other than the short rate influence the yield-curve shape.
WE’VE HEARD ACADEMICIANS AND PRACTItioners say, “This is only a theory; the data shouldn’t be expected to fit it precisely.” Most of the originators of these theories cheerfully acknowledge as much. Conversely, we’ve also heard academicians and practitioners contend, “The theory tells us that this should happen, so it will happen.” Sometimes the same person makes both points, focusing on whichever argument is the most convenient for the moment.
Theories are just theories. They help us to understand how the world should work. There’s no harm in finding that our theories are merely an approximation of the real world or in raising arguments that suggest the world works somewhat differently from the theory. Shouldn’t we be open-minded enough to question our own assumptions -- even our core beliefs -- and subject them to the rigors of empirical testing?
I’ve been increasingly concerned that our industry overall seems to have lost some focus on thoughtful analysis of finance issues. All too often investment professionals prefer to operate on the basis of heuristics or shortcuts, some shaped by theory and others by convention, rather than examine our core assumptions. Far too often these heuristics set the stage for error on a massive scale.
Some of those concerns can best be illustrated by a series of examples.
If stocks offer a 5 percent risk premium over bonds, then it makes little sense for any long-term investor to diversify away from stocks. The arithmetic is compelling. If stocks normally deliver better returns than bonds by 5 percent per year, compounded over time, the long-term investor has almost a 95 percent chance of winning with stocks by the end of a 20-year span. The cult of equities, the notion of stocks for the long run, is predicated on this lofty risk premium.
If the risk premium is smaller, the arithmetic quickly becomes less interesting. If the risk premium falls by half, the time required to have a high confidence of winning with stocks quadruples. It’s simple, but powerful, arithmetic.
Many in academia like the simplicity of a fixed risk premium, matching the historical excess return of stocks relative to bonds or cash. Simplicity is a good thing. But as Albert Einstein was fond of saying, we should seek the simplest idea that matches reality -- but no simpler! A fixed risk premium is a hypothesis, not a fact; indeed, it’s one of the least defensible hypotheses in the finance world today.
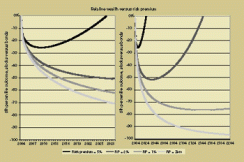
Let’s relax the assumption of a fixed risk premium. Consider the graphs on page 119, which examine worst reasonable outcomes. We define this as the 5th percentile outcome, which you have a 95 percent chance of beating. If stocks are 15 percent more volatile than bonds and have a normal excess return of 5 percent above bonds, then the 5th percentile outcome is a 19 percent shortfall. That is, we’d have a 5 percent chance of stocks underperforming bonds by 19 percent or more in a year. That’s bad, but obviously it’s not without precedent.
In the second year our 5th percentile outcome is not another loss of 19 percent. Because risk expands with the square root of time, the 5th percentile outcome is 34 percent below the mean, which has now grown another 5 percent to a 10 percent gain. So the 5th percentile outcome is a loss of only 24 percent, barely 5 percent worse than the one-year case.
In fact, with a 5 percent risk premium, the worst reasonable outcome bottoms out at a 26 percent shortfall relative to bonds after five years -- not much worse than the worst reasonable year. After the first five years, the worst reasonable scenario quickly becomes brighter. After 25 years we have a better than 95 percent chance of winning with stocks relative to bonds. The worst reasonable outcome is that we’re no worse off with stocks than with bonds. In a nutshell, that’s the basis for the stocks-for-the-long-run thesis.
But how realistic is this 5 percent risk premium today? If bonds yield 5 percent, we need to get a long-term return of 10 percent from stocks to get that 5 percent risk premium. Today stocks yield just over 1.5 percent, so stocks have to deliver long-term earnings and dividend growth of 8.5 percent to deliver that 5 percent risk premium. That’s a lot to ask: Per-share earnings growth in the 20th century (no slacker for growth, as centuries go) averaged just more than 4 percent, of which fully 3 percent was inflation.
The oft-cited stock buybacks won’t bail us out, either. In an article in the Financial Analysts Journal last year with co-author Bill Bernstein, we show that new share issuance, typically through initial public offerings and secondary equity offerings, has always sharply exceeded stock buybacks, with a brief exception during the Michael Milken years of the late 1980s.
Suppose earnings growth is only 5.5 percent, 4.5 percent or 3.5 percent. Even though two of these growth rates exceed the growth rate of the 20th century, they correspond to slender 2 percent, 1 percent and zero-risk premiums. After 25 years we’re 50 percent, 60 percent and 70 percent behind bonds and still headed south. Though this is the worst reasonable 5th percentile outcome, it’s well within the realm of possibility.
With a 2 percent risk premium, this worst reasonable outcome never gets much worse than a 50 percent shortfall and finally surpasses bonds -- in a bit under 150 years -- as the second graph opposite shows. With continuing advances in longevity, maybe our grandchildren will live to see this, but probably not.
The worst reasonable outcome with a 1 percent risk premium hits its low point about this same time, a century and a half hence, at 77 percent less wealth than the bond investors, and begins to slowly creep upward. After about six centuries a 1 percent risk premium would deliver a 95 percent chance of stocks beating bonds. The heirs of Henry V or the founders of the Ming Dynasty would still be waiting for those 95 percent odds of success to prevail.
Notably, both of these scenarios require earnings growth that is faster than we’ve seen during the past century of steadily rising prosperity. With earnings growth of 3.5 percent, we’d have no risk premium, for which the worst reasonable outcome can obviously never “hit bottom.”
Stocks-for-the-long-run works if the risk premium is high, which is far more plausible when dividend yields are high than when they are low. In an FAJ paper in 2002 with Peter L. Bernstein, we show that the normal risk premium over the past two centuries has probably been about 2.4 percent. If that’s true today -- which is doubtful with dividend yields near their two-century lows -- then the 100-year investors can expect their stocks to beat their bonds with 95 percent confidence. If the current risk premium is lower than 2.4 percent, we’d need a longer horizon to have this much confidence in the superiority of our stock holdings.
Naturally, if we are willing to settle for a 60 percent, rather than a 95 percent, likelihood of success, the time we need to wait is considerably shorter. But we’re being asked to believe, frequently by highly regarded academics, that the wait for stocks to assuredly outpace bonds is a reasonable span for patient investors. This is not true unless stocks are priced to deliver a high risk premium over bonds.
| Arithmetic of compounding |
MANY INVESTORS ASSUME DIVIDENDS don’t matter if the growth is sound and management is reinvesting wisely for the future. After all, dividends grow over time; bond coupon payments do not. Eventually, the former surpass the latter, forming the basis for the superiority of stocks -- for the long-term investor. Furthermore, Miller and Modigliani have taught us that lower dividend distributions should deliver faster earnings exactly sufficient to offset the lower dividend yield.
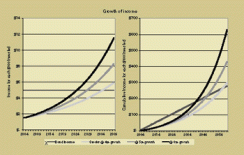
How long must we wait before our income on stocks matches our income on bonds? Consider the graphs on page 120. Today $100 invested in bonds delivers about $5 of income; in stocks it delivers roughly $1.50. If dividend growth merely matches the 4 percent rate of the 20th century, then in 32 years our dividend income catches up with the income we’re earning on bonds. If growth is more robust, at 5 percent or 6 percent, the wait is shorter, at 26 and 22 years. This is a long wait, but so far so good; the patient investor eventually wins with stocks.
How long do we wait for the cumulative income to catch up? (Thanks to Peter Bernstein for suggesting this simple yet powerful question for better understanding the nature of the equity risk premium.) If we see solid dividend growth of 5 percent or 6 percent, we need 44 or 37 years. If dividend growth matches the 4 percent growth of the 20th century, we need a startling 54 years for our cumulative income to have kept pace.
In those 54 years our $100 bond investment will have paid us $270 (assuming we can reinvest at the same 5 percent when today’s bonds mature), and our stocks will have finally paid us $274. The long-term investor eventually wins, but it’s a daunting wait.
These graphs vividly show us what a skinny risk premium looks like. The risk premium rules of thumb that we’ve been taught to rely on are shaky indeed. Peter Bernstein has a wonderful article scheduled for the FAJ early next year in which he likens today’s low yields to frozen orange juice. He reminds us that we are so accustomed to frozen orange juice that many of us forget how much more satisfying fresh orange juice can be -- as with stocks that allow their investors to share in the earnings sooner rather than later, through direct (and now tax-advantaged) cash distributions.
Respected academics have suggested that:
* If dividend yields are below historical norms, then the market is clearly expecting faster future growth. With this circular logic, we may as well buy at any multiple, since our buying creates still-higher multiples and the resulting lower yields will imply faster future growth.
* If payout ratios are below historical norms, the retained earnings will be reinvested in projects that will lead to faster future growth. Again researchers invoke Miller-Modigliani. If that shortcut is sound, why not encourage management to retain all the earnings? After all, the massive investments over 19982001, funded out of retained earnings, certainly must have led to a major step-up in subsequent earnings growth rates, right? Tell it to the telecommunications investors of those years. A careful examination of the data provides no support for this intertemporal interpretation of Miller-Modigliani.
Aren’t these arguments based on the inverted logic that because our best finance models are reliant on certain assumptions, then for the models to be correct, the assumptions must be right, too? Miller-Modigliani developed a brilliant thesis, which proves that dividend policy and structural debt and equity decisions don’t matter -- so long as investors are rational, there are no taxes, managers operate in the best interests of the shareholders, borrowing and lending are at identical rates and so forth. Surely, there’s no harm in assuming these assumptions are correct?
As the graphs on the next page vividly illustrate, today’s investors have to wait about a half century to find out if this circular logic prevails. Alternatively, we can rely on common sense. If the models are based on selective assumptions, let’s examine the validity of those assumptions before we accept the dictates of the models as truth.
WHY DO WE SO READILY ACCEPT FORECASTS based on extrapolation from the past? If bond yields fall from 8 percent to 4 percent and the bonds thereby deliver a 15 percent annualized return, should we assume 15 percent as a future bond return? Of course not. The capital gains that push our 8 percent yield up to a 15 percent return are nonrecurring.
Should we “conservatively” assume continued capital gains of 7 percent per year on top of our new 4 percent yield? Of course not. Yet much of our industry, with an assist from assorted academic luminaries, is wedded to forecasting equity returns in this fashion.
Returns are for the most part a function of simple arithmetic. For almost any investment, our total return consists of yield, growth and multiple expansion or yield change. For bonds, the growth is simple; fixed income implies zero growth. For high-yield or emerging-markets debt, growth is negative, because of the occasional defaults. For stocks, growth tends to be about 1 percent above inflation, according to very long-term history.
The 7 percent real stock market returns for the past 78 years covered in Ibbotson data consist of roughly 4.3 percent from dividend yield, just over 1 percent from real dividend growth and 1.5 percent from multiple expansion. So why can’t we expect 7 percent in the future? We can’t rely on multiple expansion because the market isn’t cheap by any conventional definition. At a minimum, most observers would subtract multiple expansion from future return expectations. Now we’re down to about 5.5 percent.
But our current dividend yield is currently just 1.6 percent, not 4.3 percent, which takes our real return down to about 2.5 to 3 percent. And that’s without any mean reversion toward historical valuation levels. Much of our industry seems fearful of simple arithmetic of this sort, preferring to forecast the future by extrapolating the past.
WHY IS A LOW (EVEN NEGATIVE) RISK PREMIUM considered shocking? There is nothing in the legislative code that assures a positive risk premium, yet the notion of a negative risk premium view seems downright scandalous to our industry. There is no reason, beyond finance theory, to believe that a temporary negative risk premium should be impossible. Only finance theory suggests that this should not be possible (if investors are rational, if there are no taxes, if utility functions flatten with increasing wealth and so forth). But finance theory would also demand rational investors to shun lotteries and casinos.
Should there be a positive equity risk premium relative to bonds? Of course. Is it written into contract law for any assets we buy? Of course not. In the long run, the market should adjust to provide a positive expected risk premium, or else why buy the riskier asset for a lower return? But the adjustment to a positive rationally expected risk premium can be painful.
A 5 percent risk premium is often taken as fact, but it’s only a hypothesis and often an ill-reasoned one at that. If we take a 5 percent risk premium as a fact rather than a hypothesis, we are free to focus on asset selection, as we’ve now dispensed with the risk premium and by extension the resulting asset-mix decision.
Even the most aggressive, intellectually honest forecasts of long-term earnings or dividends growth would see gross domestic product growth as an upper bound. But GDP growth has two engines: the growth of current enterprises and the creation of new enterprises through entrepreneurial capitalism. Our stock market investments allow us to participate in the former but not the latter. Because more than half of real GDP growth comes from entrepreneurial capitalism, real earnings and dividends should collectively grow a bit under half the rate of economic growth.
Surprisingly, consensus long-term earnings growth estimates routinely exceed sustainable GDP growth. The current consensus growth rate for earnings on the Standard & Poor’s 500 index, according to Bloomberg, is 10 percent, which corresponds to 7 to 8 percent real growth, assuming the consensus inflation expectation of 2 to 3 percent. Real earnings growth of 8 percent is six times the real earnings growth of the past century and three times the consensus long-term GDP growth rate. This is not possible unless either GDP growth quadruples or stock buybacks exceed new share issuance by an unprecedented margin. Otherwise, aggregate earnings would eventually exceed our GDP.
GDP growth, less the economic dilution associated with entrepreneurial capitalism, basically defines the sustainable growth in per-share earnings and dividends. Accordingly, it is hard to imagine that stocks offer a positive risk premium when they are yielding far less than inflation-indexed government-guaranteed bonds (Treasury inflation-protected securities, or TIPS). Yet this was the case in December 1999 and January 2000.
At the start of 2000, stock market yields were a scant 1.1 percent, while the TIPS yield was 4.4 percent. Earnings and dividends would have needed to grow 3.3 percentage points per year (triple the real growth rate of the prior century) for stocks to merely match the total return of TIPS. Was there a negative risk premium (at least for broad stock market averages, relative to TIPS) at the beginning of 2000? In my own view, the answer to this is obviously yes -- but no one wanted to believe it.
Many market observers would agree that the cult of equities -- the reliance on a 5 percent risk premium -- represents the single most damaging error in the institutional sponsor community in the past quarter century. Shouldn’t our industry, as a matter of course, question aggressive and unsustainable growth forecasts before acting on them?
A closely related question is, why do we accept rising return expectations in a rising market? In 1982 the average pension return assumption was barely 6 percent. This was at a time when stock yields were 5 percent and both earnings yields and bond yields were in double digits. By 2000 the average pension return assumption had risen to approximately 9.5 percent, even though stock dividend yields were down nearly 400 basis points and bond yields down 800 basis points. Now that markets have fallen, we’re seeing pension return assumptions drifting downward again!
If we see bond yields fall 800 basis points, fueling substantial capital gains on top of a substantial initial yield, do we assume that the future returns will be better because the bonds exceeded expectations? No, we’ll be grateful for the returns of the past and expect less, not more, in the future. Why can’t we use the same logic in equities and other asset classes?
WHAT SPENDING CAN OUR PORTFOLIOS sustain? Many of the recent problems in the newly underfunded pension, endowment and foundation world stem from 1) return expectations that are unrealistic and 2) a desire to spend more than market returns can support. A need for a particular rate of return, or a hope for performance that can sustain outsized spending, does not allow us to expect that return.
How do we define wealth? Is it the size of our portfolio? No. A century ago a $1 million portfolio was huge; today it’s assuredly not. Is wealth defined as the real (inflation-adjusted) value of our portfolio? Not really. Spending needs change, and the real returns that our portfolio can sustain will change over time. Even though the consumer price index has risen 20-fold over the past century, a $20 million portfolio will not sustain the level of real spending that a $1 million portfolio could sustain in 1904. Why? Because real yields are lower.
A better, although still imperfect, definition of wealth is the real spending that our portfolio can sustain over the span that the portfolio is intended to serve. An 80-year-old with $1 million is far wealthier than a 40-year-old with $1 million. A $1 billion pension fund can sustain larger payouts than a $1 billion endowment or foundation because of the finite life of pensioners (hence of current pension obligations).
Our industry pays scant attention to the concept of sustainable spending, which is key to effective strategic planning for corporate pensions, public pensions, foundations, endowments and even for individuals. Sustainable spending typically starts with sustaining the real value of the assets. This requires realistic return assumptions.
We need to know how much we can spend on a near-risk-free basis in order to know how much of our intended spending comes from wishful thinking -- from hope. This exercise sets the stage for a reasoned, risk-controlled quest for the incremental returns that we “hope” to achieve. Finance theory has paid this whole subject little heed.
Sustainable spending is not a fixed rate on assets. It changes as real yields change. Most foundations and endowments have used a 5 or 6 percent spending rule for many years. The capital markets have sometimes been priced to make this an easy goal, and sometimes (like now) a very difficult one. For the same reasons, pensions cannot hope to duplicate the 1990s experience of replacing pension contributions with pension fund returns.
In recent years many otherwise sophisticated institutional investors have taken the view that they need a higher rate of return than the return that is assuredly available in the lowest-risk strategies (long-laddered Treasury bonds for most pension funds or long-laddered TIPS portfolios for endowments and foundations) and therefore need more in risky assets to earn their risk premium, based on the dangerous assumption that higher risk will lead to higher returns.
If we cannot be assured of a substantial risk premium, isn’t it better to commit to a spending stream that we can assuredly earn, boosting that spending only as future happy surprises increase our sustainable spending? Of course, this option isn’t available for foundations that must spend 5 percent each year. Alternatively, as a fallback, shouldn’t we at least acknowledge that we’re spending future investment returns that we may or may not earn?
For example, if we can assuredly earn a real return of 2 percent and want to spend 5 percent, then we need to find an incremental 3 percentage points. This must come from 1) a risk premium earned on our selected departures from our risk-minimizing portfolio, 2) alpha from our superior choice of investment managers and strategies or 3) additional contributions to our asset base.
Today the average corporate pension fund is using a pension return assumption a bit over 8.5 percent in its earnings statement, and the average public fund is using a discount rate of about 8 percent. With the bond markets yielding about 5 percent, and with most funds having about 30 to 40 percent in mainstream bonds, this means that most sponsors are expecting to earn an additional 10 percent on their nonbond assets -- a 5-percentage-point increment over bonds -- either from the equity risk premium or from alpha.
It is the conventional view that there is a high risk premium for equities and other risky assets; many sponsors expect to make up some of the difference with riskier assets. But the current risk premium cannot be assessed by looking at past excess returns. This would lead us to boost our expectations at market tops and reduce them at market bottoms.
We can look at the building blocks of return. As we’ve already demonstrated from current market levels, we do not find a large risk premium in most of the markets that we typically rely upon for this extra return.
| Returns adjusted for yield changes |
Alpha is the incremental return earned above broad market benchmark returns as a consequence of manager skill. Because institutional investment managers essentially are the market, the average alpha earned by the managers must be reasonably close to zero. If almost all corporate and public funds are willing to assume alpha as part of their return stream, then they must, like the citizens of Lake Wobegon, all be above average.
The sensible view on alpha is to seek it, to be grateful when it is earned reliably over time but not to assume it as part of the normal course of investing. Why does our industry shackle itself with return expectations that include a material alpha when by doing so we set ourselves up for a fall? If we earn 1 percentage point above a realistic benchmark, our clients and our directors are angry because we didn’t achieve our 2 percent target alpha rather than grateful that we achieved 1 percentage point that other investors didn’t earn.
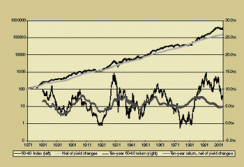
For simplicity, we consider a simple passive 60-40 asset mix as the basis for our analysis. The return for such a portfolio can be seen in the graph on page 121, earning a lofty 380 times our starting wealth in 132 years. That cumulative return consists of three parts: income (the lion’s share of return for both stocks and bonds, as we have previously demonstrated), growth in income and changing valuation levels. The last is an important part of our monthly or yearly returns but cannot be presumed to play a major role in our long-term return expectations. As John Maynard Keynes said, “Trees do not grow to the sky.”
We can easily strip away that last component of returns simply by assuming that the best guess for the future bond market yield is the current bond market yield; the best guess for the future stock market yield is the current yield; and the best guess for the future price-earnings ratio for the stock market is the current price-earnings ratio. This leads to the smooth line, roughly matching the cumulative return for our 60-40 asset mix.
In a fundamental sense, the return associated with this smooth line can be viewed as a measure of the sustainable return, which is the key driver for sustainable spending, for our 60-40 mix. Because we’re stripping away the portion of return associated with changing valuation levels, we’re focusing on the returns associated with yield and growth -- the only elements of return that we can rely on in setting sustainable return expectations or sustainable spending.
The graph becomes even more interesting when we look at the rolling ten-year returns for both lines. For instance, the return for a 60-40 mix for the ten years ended December 2003 was 8.3 percent. Not bad. But if stock and bond valuation levels hadn’t risen over that decade (that is, if yields had not fallen), the return would have been 5 percent. So 3.3 percentage points of the annual return for a 60-40 asset mix over the past decade was because of rising price-earnings ratios, falling dividend yields and falling bond yields, which we dare not rely on for setting our return expectation or our spending plans.
At other times, the return on a 60-40 mix has fallen far short of the return net of yield changes. For instance, in the decade ended December 1974, a 60-40 investor would have seen a negative return of 0.7 percent, while that same return rises to 4.7 percent per year if we strip out the effects of falling price-earnings ratios and rising yields.
The rolling ten-year returns have ranged from 1.3 percent (the decade ending September 1974, with real returns lower still) to a 15 percent gain (through July 1992). When we strip out the portion of return associated with changing valuation levels, however, we find a much narrower range, averaging 5.7 percent, with a standard deviation of just 1.3 percent. The extreme outliers of the past half century were 4.5 percent to 7.8 percent.
Current pension return assumptions and public fund discount rates of 8 to 9 percent have never appeared in the entire history of this series. To achieve those returns, these sponsors are relying on either falling yields, rising price-earnings ratios, outsized alphas or unprecedented growth rates to garner the returns that they “require.”
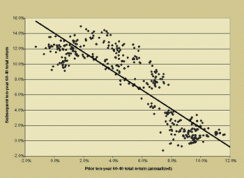
Mean reversion is widely evident in this data. When we compare our ten-year rolling return for the 60-40 passive mix with the nonoverlapping prior ten-year return, we find an 85 percent negative correlation between one decade’s return and the subsequent decade’s return, as we can see in the graph below.
The mean reversion is less powerful if we look at the full 133-year span, but it is still a daunting factor. It shows up in both a mean reversion in our sustainable return measure, which strips out the return from valuation level changes, and in the excess returns earned by those same valuation level changes.
While I disagree with many elements of Jeremy Siegel’s Stocks for the Long Run, I commend him for recognizing that this mean reversion reduces the risk of equities for the long-term investor. It’s a puzzle that he doesn’t as readily acknowledge that, following the largest equity revaluation in history, from 19822000, mean reversion might exact a toll from future returns.
Converting the numbers to real terms, we find a like situation. The rolling ten-year real return from a 60-40 mix has averaged 4.2 percent since 1871, but some of this return can be traced to falling yields and rising valuation levels. Net of these effects, we find an average real return of 3.4 percent for a 60-40 balanced portfolio. In the past half century since 1953, the ten-year real return for a 60-40 portfolio has averaged 3.3 percent, which drops to 1.9 percent if we strip out the effects of rising valuation levels and falling yields. None of these figures is anywhere near the 5 percent spending required of foundations. Nor does it approach the 5 to 6 percent spending rules that prevail for most endowments.
Now consider the taxable investor. Over the past 50 years, historical real returns for a 60-40 balanced portfolio have averaged 1.9 percent once we strip out the effects of falling yields and rising valuation levels. Given today’s lower yields, we cannot reasonably expect more. So as we are eventually taxed on both the real return and the inflation component of our return, it is reasonable for the taxable investor to expect a real aftertax return fairly close to zero.
This makes the arithmetic for taxable investors remarkably simple. If a retiree wants to maintain a lifestyle costing $40,000, adjusted for inflation, with a life expectancy of 25 years, he or she will need $1 million to sustain that. If the actual real aftertax returns are higher, then the retiree can improve on that lifestyle. We have not done a good job of conveying this message, or anything near it, to our taxable clients.
If we spend above a sustainable level, we must make up the difference in contributions -- unless we earn that increment from a sensible risk premium or from alpha.
For corporations, this means they must contribute (gasp!) to help fund each new year’s growth in future pension obligations. By fiddling with liability discount rates, the government may help companies push this requirement out a few years more, but this only increases the burden on future generations of management and compromises the security of the future generations of pensioners. The corporate pension community got spoiled in the 1990s with long contribution holidays, which fostered the illusion that pension plans require no contributions to meet their obligations.
For endowments, capital campaigns may be needed to top up the assets, and to cover any spending that exceeds the risk-minimizing real yield offered by the markets. The bull market of the 1980s and 1990s allowed us to accept a 5 percent spending stream as a seemingly conservative choice, even though the lofty real returns during these decades benefited considerably from revaluation, not from the sustainable components of return, income and growth.
For foundations, which typically have no source of supplemental contributions, this means they ultimately might not earn the 5 percent real return required to maintain the real value of the corpus of the foundation portfolio. That is, most foundations, while enjoying a very long life span, may not fulfill their intended role as a perpetuity serving the goals of the founder forever.
For the long-term investor, return expectations of 8 to 9 percent can’t be achieved in a world of stock yields below 2 percent and bond yields of 5 percent. If the intended spending rises with inflation, as it often does, then sustainable spending falls well short of 5 percent, absent contributions.
None of this can be comforting to those who would like to rely on lofty return assumptions to justify chunky spending or skinny contributions. But it is far better to plan for the future on assumptions that are sound rather than to rely on hope as our strategy for the future. The same applies to the individual investors planning for their future retirement; working a few extra years to contribute more to our retirement reserves is better than running out of money when we can least afford it, as a consequence of foolish or unrealistic assumptions.
FIDUCIARIES, SERVING OTHERS AS ASSET managers, face risk as an ill-defined concept: Risk is whatever goes wrong, which we cannot know until after the fact. Most risks that we face as fiduciaries fall into three broad categories:
* Risk of falling short relative to a preselected normal portfolio (or benchmark).
* Risk of failing to meet obligations or liabilities because of asset-liability mismatch.
* Risk of losing money, either in a portfolio or in one spectacularly failed investment.
The mathematics of finance cannot easily work with a multidimensional definition of risk, even though the dynamics of investment committees can react to any of several risks. So finance theory and practice pull us in different directions in our definitions of risk.
Finance theory tells us that a lognormal return distribution fits reality reasonably well and can be used to derive an array of interesting models for market behavior. If returns are lognormally distributed, we can value our options with precision (Black-Scholes); we can optimize our portfolios to maximize return at any given level of risk (Markowitz); and we can parse returns into a host of useful risk metrics (Fama, French, Roll and Ross). All of this points to a lognormal standard deviation as the basic metric of risk.
Markowitz also demonstrated that kurtosis (a measure of the fat tails of a distribution) is more likely to be infinite than to match the measured kurtosis. Yet even the measured kurtosis already wreaks havoc in valuing far-out-of-the-money options with the Black-Scholes model. So even this simple measure of risk falls short.
Meanwhile, most of our clients focus on benchmark risk: How are we doing compared with some preselected benchmark? If we manage stocks, we want to know whether we beat the S&P 500 or a Russell index. If we manage a pension fund, we want to beat a passive 60 percent equity/40 percent bond mix. And we are asked how we rank relative to our peers. But benchmark risk is only part of the picture.
Peter Bernstein lowered the boom on the policy portfolio in May 2003, triggering an anxious and sometimes heated debate on the riskiness of the long-term, static policy portfolio -- for example, a portfolio of 70 percent equities/30 percent bonds -- so embedded in much of the institutional investing world. He suggested that policy portfolios are overused and misused and often lead to a singular focus on an irrelevant metric of risk, our tracking error relative to a policy portfolio or relative to our peers. This one-dimensional view of risk has cost the pension community hundreds of billions of dollars since 1999.
Worse, the other measures of risk, notably the asset-liability mismatch, have punished us even more severely. The liabilities of most pensions behave like long-duration bonds, and the obligations served by most endowments and foundations behave like TIPS. Both long bonds and TIPS rose roughly 50 percent during 2000'03. If our assets are down as much as 20 percent and our liabilities are up 50 percent, we have a problem.
Benjamin Graham was fond of saying that the essence of investment management is the management of risks, not the management of returns, because we can gauge what risks we are taking but cannot know what returns we will earn. Accordingly, we should consider policy asset mix from a risk perspective while ignoring past recent returns.
Our simplistic view of risk cries out for change -- in favor of a multidimensional view of risk, avoiding unacceptable outcomes on multiple dimensions. This approach does not proscribe stocks or other risky assets; rather, it suggests that we have reasonable expectations and recognize that the cult of equities provides assurances that we cannot rely on. A multidimensional view of risk favors 1) the less-correlated assets to cut our risk and 2) assets that can diminish the mismatch between our assets and our liabilities.
Stocks are an important element in our toolbox, but from the perspective of a long-term investor, the advocates of equitycentric investing overpromise what stocks can deliver.
| Mean reversion in 60-40 returns: 1944-2003 |
Investment committees are often given answers to a handful of important questions. How much is our portfolio worth? How much did it go up or down last year (or last quarter or last month)? How did it perform relative to its peers? Yet other questions are rarely explored. Before the bubble burst, few investment committees asked how their portfolios performed last year relative to their liabilities.
If returns had been measured relative to the cost of defeasing obligations at an assured market yield (that is, the yield of the laddered strips or TIPS that could immunize the future obligations), the disaster of 2000'02 could have been mitigated or even avoided.
If we share multiple dimensions of risk with our investment committees, we are less likely to surprise them with results that, while acceptable relative to peers, are disastrous relative to liabilities or against a simple real return target. If we show our performance, and our risks, relative to these additional metrics, boards can make better decisions on their investment portfolios.
We should also encourage our investment committees to examine our risks. What’s our worst likely outcome (for example, value at risk, or VaR) in absolute returns, in returns relative to our peers or in returns relative to our liabilities?
Suppose an investment committee sees that, in a worst reasonable (95th percentile) three-year span, the portfolio could fall by 25 percent, could lose 35 percent relative to the liabilities or could lose a scant 6 percent relative to peers. How many committees would remain so closely shackled to the peer group in the face of such evidence? Yet this is the typical situation today, in pensions, endowments, foundations and the defined-contribution-plan holdings of our employees.
The literature of behavioral finance explores multiple dimensions of risk, acknowledges human frailty and studies the excesses engendered by fear and greed. Many of the weaknesses of classical finance theory that I discuss are really manifestations of behavioral finance, evinced in the actions of the institutional investing community. Unfortunately, behavioral finance provides few tools to help us manage assets better, so many in the finance community either dismiss it or, at best, are unsure what to do with it.
From the perspective of the practitioner, behavioral finance tends to be ignored because it doesn’t offer us simplifying shortcuts for our key asset management decisions. Perhaps we should ask why we ask finance theory to provide shortcuts.
WE CANNOT RELY ON FINANCE THEORY,brilliant as its findings may be, as a shortcut to easy answers. We point to Miller and Modigliani to reassure ourselves that 70 percent and even 100 percent earnings retention is fine, because the retained earnings are surely being used to fund innovations that will lead to unprecedented future growth. We point to the CAPM to compute expected rates of return and to assess the alphas of our strategies. We point to Black-Scholes and VaR to show that we don’t face an unacceptable worst-case outcome. Long-Term Capital Management learned the hard way (and showed us) that returns and alphas are not lognormal and that mean reversion can work on a scale that outlasts one’s capital.
Behavioral finance helps us understand how human frailties can create the very market behaviors that classical finance theory seeks to explain away -- but it can’t seem to help us decide how to profitably invest.
There is too much complacency in our industry, both in the academic and the practitioner communities. Too many people say, “Assuming this, then we can decide that"; far too few are willing to directly question their basic assumptions. As fiduciaries, we owe it to our clients to be less accepting of dogma and more willing to explore the implications of errors in the root assumptions of finance theory. These basic assumptions often fail when they are tested. There’s nothing wrong with our assumptions failing -- that’s where the profit opportunities can be found.
Our theories describe how the world should work. Advances in finance theory can help us to better understand that world. We know Arbitrage Pricing Theory and Fama-French advanced our understanding of portfolio risk and of the return-generating processes at work in our investments, representing an important step forward from the single-factor capital asset pricing model.
When theories do not agree, though, should we discard the messier one? Not if we accept the wisdom of Einstein, requiring our theories to be as simple as possible but no simpler than necessary. If finance theory assumes that markets are efficient and behavioral finance suggests that markets are not efficient, do we discard the less convenient theory? All too often our industry does exactly that.
Isn’t it better to recognize that there are elements of truth in seemingly incompatible theories? If we do so, we gain a richer understanding of the markets where we seek our clients’ profits and our livelihood, but if we confuse theory with reality -- if we accept the root assumptions of theory as fact -- we can fall into catastrophic errors. Such is the origin of the cult of equities, with consequences that may ultimately be measured in trillions of dollars.
Far too few recognize that we can profit from the gap between theory and reality, often far more readily than by accepting theory at face value. Here lies one of the untapped benefits of our best theories.
Peter L. Bernstein, the founding editor of the Journal of Portfolio Management, writes that “one of the more interesting developments” in JPM‘s evolution was the arrival of papers from “unknown young people” like Robert D. Arnott who “had important contributions to bring our way.” A theoretician and practitioner, Arnott, 50, is chairman of Research Affiliates in Pasadena, California, and has contributed more than 60 articles to scholarly journals and is himself the editor of the Financial Analysts Journal. A summa cum laude graduate of University of California, Berkeley, Arnott was chairman of First Quadrant, president of TSA Capital Management, vice president of Boston Co. and global equity strategist for Salomon Brothers.
