“MORE RISK, MORE EXPECTED REWARD.”
If you naively applied this central principle of financial theory to investing in equities over a 40-year career, you’d probably want to hold a portfolio consisting mostly of high-risk stocks. Given your long time horizon, the extra volatility most likely wouldn’t be a problem. You might start by buying a diversified collection of the most volatile stocks within an investable universe such as the Standard & Poor’s 500 Index. Once in a while, you’d look at your portfolio and find that some of your stocks had low volatility or had dropped outside the investable universe, so you’d replace them with newly available high-volatility stocks to stay true to your investment style. (Stock volatility here is measured on an absolute basis, not relative to a benchmark.)
To your horror, you would have significantly underperformed a cap-weighted index portfolio even within a decade. Adding insult to injury, holding the low-volatility stocks would have been better still. What’s going on here?
The historical performance of different asset classes over the long term is indeed consistent with the rule of thumb that greater risk leads to greater reward. However, it appears that this principle does not extend to individual equities. Many academic studies, as well as historical backtests of low-volatility indexes, indicate that portfolios composed purely of low-volatility stocks tend to outperform portfolios of high-volatility stocks over the long term. This phenomenon is usually interpreted to imply that low-volatility stocks have higher returns, on average. As this flies in the face of standard ideas about asset pricing, it is usually referred to as the “low-volatility anomaly.”

How can we tell if the low-volatility anomaly is the result of individual stock behavior or portfolio rebalancing effects — or both — and why should we care? In a nutshell, the rebalancing explanation would provide more confidence that past observations will persist in the future. This insight has more than merely academic interest. Billions of dollars have flowed into low-volatility equity portfolios over the past few years. For instance, by 2011 pension funds and other institutions had invested almost $10 billion in low-volatility U.S. equity strategies, up from virtually nothing in 2005. The story has been similar outside the U.S., with more than $6 billion invested in low-volatility equity strategies in continental Europe alone. Index providers such as MSCI, Russell Investments and S&P offer low-volatility indexes. On the retail side the most popular new exchange-traded fund in the U.S. for 2011 was a low-volatility strategy designed to replicate the S&P 500 Low Volatility Index.
It is easy and tempting to dismiss low-volatility equity strategies as a fad. Only time will tell, but in our opinion, the category merits considerable attention, as these strategies may indeed offer superior risk-adjusted returns than capitalization-weighted indexes. The low-volatility equity products offered today — and there are frequently new ones — generally fall into one of two categories: portfolios composed of low-volatility stocks and equity portfolios with low volatility.
Portfolios of the first type are generally constructed by selecting the least volatile stocks from an eligible universe, then combining them in some manner. There may be fundamental or quantitative overlays, and possibly some risk control in the choice of stock weighting. Because correlations are not always taken into account during the stock selection process, the overall portfolio volatility may be higher than one might expect, but it should still be lower than the volatility of a cap-weighted index. The S&P 500 Low Volatility Index is an example of a benchmark that tracks the hypothetical value of a portfolio of this type.
The second category includes minimum-variance portfolios. They are constructed by a methodology that seeks to lower or minimize the overall portfolio variance. MSCI’s Minimum Volatility indexes are an example of such an approach, which generally addresses portfolio risk in a more effective manner than portfolios of low-volatility stocks because lowering that risk is specifically targeted. Many proponents of low-volatility portfolios attribute their historical and simulated outperformance versus cap-weighted benchmarks to the low-volatility anomaly. However, these portfolios typically include some high-volatility stocks that have low correlations to the other stocks in the portfolios. This means that the low-volatility anomaly, as described above, is unlikely to fully account for the performance of such portfolios. Instead, optimizing to minimize the volatility may well be expected to provide a more efficient portfolio than the cap-weighted index.
Interest in low-volatility-type equity strategies, which comprise both of the above classes of portfolios, has never been higher. Regardless of the specifics, these strategies are widely perceived to exploit the low-volatility anomaly. Indeed, they are often advertised in exactly this way, prompting reactions ranging from enthusiastic acceptance to outright skepticism.
It’s hard to argue that a portfolio-level phenomenon isn’t real: Papers noting the existence of the low-volatility anomaly appeared as early as the 1970s. It is easy to confirm that portfolios of high-volatility stocks have underperformed portfolios of low-volatility stocks over the long term. These findings have been replicated in studies of markets in many different countries.
Finance academics and practitioners have advanced many explanations for these findings. They tend to fall into two categories: stock mispricing and systematic risk factors. Mispricing — meaning that high-volatility stocks are overvalued relative to low-volatility stocks — is sometimes attributed to behavioral effects. For example, overconfidence and irrational preference for lotteries may lead to demand for high-volatility stocks greater than that indicated by the stocks’ fundamentals. The fact that the resulting mispricing isn’t arbitraged away is attributed to lower liquidity in low-volatility names or to the benchmark-centricity of institutional investors, creating a limit to the amount of capital that can flow into lower-beta stocks. These effects are hard to quantitatively verify, however, and fail to explain the presence of the anomaly in the historical data for time periods before benchmarks were in common use or when investors had higher risk aversion. Systematic risk factors may be based on actual volatility or idiosyncratic (beta-adjusted) volatility; exposure to these factors would contribute to future lower returns. The rationale for the existence of these risk factors is less clear. In none of these cases are any portfolio-level effects, such as return contribution as a result of rebalancing, taken into account.
Diversification into varied risky assets helps in this regard. When multiple stocks are combined in a long-only portfolio, their interaction actually causes the portfolio to have a higher compound growth rate than the weighted average compound growth rate of the stocks in that portfolio. The difference in growth rates is usually small for concentrated, infrequently traded portfolios. For diversified, regularly rebalanced portfolios, this difference can amount to hundreds of basis points per year. (The difference between portfolio and stock compound returns, or “excess growth rate,” was first explained in a 1982 paper by Robert Fernholz and Brian Shay, giving rise to the discipline of Stochastic Portfolio Theory. The phenomenon has subsequently been independently rediscovered several times and is sometimes known as “volatility pumping” or “diversification return.”)
The full impact of diversification and rebalancing on compound returns can be quantified using highly technical mathematics. Fortunately, the low-volatility anomaly can be analyzed using much simpler techniques. Let’s focus only on the impact on portfolio returns of the simple requirement that whenever we trade a portfolio, we are allowed to hold stocks only within the investable universe. Suppose that this universe consists of the 1,000 largest stocks (by capitalization) in the U.S. market. If we hold a stock that drops out of the universe, we will certainly be selling it at a relative loss, because the stock has failed to keep up with the other stocks. After all, it has lost its place in the top 1,000. In essence, the strategy requires that we sell low in this case, creating a drag on performance.
Of course, even a cap-weighted index of the same stocks is subject to this reconstitution drag. The question is, do portfolios of low-volatility stocks have less drag than the index? There is good reason to believe that they should and, furthermore, that portfolios of high-volatility stocks have more drag than the index. Everything follows from the basic observation that low-volatility stocks have less variability of outcomes, while high-volatility stocks have more variability. The effect on the reconstitution drag should be as follows:
• Low-volatility stocks tend to move less in price than the average stock, so there is less risk of them dropping out of the universe than the average stock. On the other hand, high-volatility stocks have a higher risk of dropping out than the average stock.
• When a low-volatility stock does drop out of the universe, it is likely to fall less than the average stock. The opposite is true for a high-volatility stock.
• Low-volatility stocks are probably larger in capitalization, therefore less likely to drop out of the universe than the average stock. Conversely, high-volatility stocks are typically smaller in capitalization, therefore more likely to drop out of the universe than the average stock.
To get some sense of the effects of the reconstitution drag on performance, let’s imagine investing in a very simple strategy in which we buy and hold a single stock, replacing it only when it is no longer in the investable universe at the time of reconstitution. To simplify the situation even further, we’ll define this universe as consisting of stocks with capitalizations greater than $10 billion, and we will assume a monthly reconstitution. We start with one such stock. At the beginning of every subsequent month, there are two possibilities:
• The market capitalization of the company remains above $10 billion: Continue to hold the stock.
• The company’s market capitalization has dropped below $10 billion: Sell the stock and use the freed capital to buy the stock of the company whose market capitalization has most recently risen above $10 billion.
Not knowing anything further about the stocks involved, it is impossible to say what the short-term performance of this investment strategy will be. However, over many decades most large companies eventually falter for one reason or another. Whenever that happens for the stock being held, the strategy is to sell the stock at a loss and buy another stock after it has risen in value.
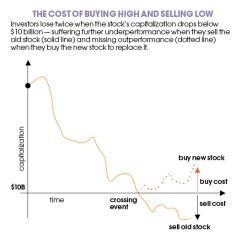
How much will this sell-low-buy-high trading hurt long-term portfolio performance? One way to think about it is to decompose the past monthly return of the stock into two pieces: the part that drove the capitalization down to $10 billion and the part that drove the capitalization even lower (see figure, above). It’s not fair to include the first piece in the cost analysis. Had the stock gone down so that the market capitalization was exactly $10 billion, we would have held on to it for another month, during which time it may have recovered. Instead, it is the excess negative return — labeled as “sell cost” in the figure — that really hurts. Moreover, the replacement stock was likely bought at a premium above the $10 billion threshold, contributing to the overall cost.
As a very long-term investment, this strategy is dubious at best: It can only work if the stock held never drops below $10 billion and will suffer greatly from reconstitution drag otherwise. The short-term performance will be poorest when the identity of the stock changes every month, as we will be losing money on every trade. If the stock we are holding is of high volatility, this is more likely to happen.
Of course, a single stock could go years, even decades, without dropping below the $10 billion threshold. We can speed up the process by investing in many stocks, which at the same time will allow us to cast new light on the persistent long-term underperformance of the megacap stocks with respect to broader stock indexes. Suppose we hold the largest 100 stocks at cap weight. Keeping the same monthly rebalancing schedule, we therefore sell the stocks that have dropped out of the top 100 at the end of the month and buy the stocks that have come into the top 100. This diligent rebalancing keeps us true to our megacap style, but it is also the sort of sell-low-buy-high trading that hurts the performance of the single-stock strategy. How much is the reconstitution drag in this case? For each stock that drops out of the universe, we can estimate the negative impact beyond the reconstitution boundary as follows:

This quantity will be zero if the stock ends up exactly as the 100th largest; any greater drop makes it negative. This return should be multiplied by the capitalization weight of the stock at the beginning of the month and summed over all dropped stocks. However, this only accounts for the sell-low portion of the drag. The buy-high aspect is the result of buying into stocks that have recently outperformed and missing the chance to participate in that growth. Implementation and market structure details can affect the precise amount this premium contributes to the cost, but it can be reasonably approximated as equal to the sell-low cost. We arrive at an estimate of the total cost of rebalancing in the prescribed fashion by doubling the amount described above for the “sell-low” portion.
In the U.S. market over the period January 1964 through November 2011, the number of stocks that have dropped out of the top 100 has typically been only two to five each month. The total portfolio weight involved is typically between 0.5 and 2 percent, and has never been more than 5 percent in a month.
If our investment universe consists of the top 1,000 stocks, the above formula can be appropriately modified. In this case more stocks fall out (typically 15 to 30 per month), but the weights in these stocks are very small. Indeed, the total weight of these stocks exceeded 0.7 percent only during the crises of 2000 and 2008. As a result, we shouldn’t be surprised to see that the reconstitution drag for the top 1,000 stocks is smaller than that for the top 100 stocks. In fact, the drag on performance for the top 100 is 81 basis points a year greater than that for the top 1,000. This is comparable to the 85-basis-point-a-year average compound outperformance the top 1,000 stocks experience over the top 100.
Our first conclusion, and there is plenty of other evidence to support it, is that the long-term outperformance of the broader index over its concentrated megacap cousin has little if anything to do with individual stock return rates. Instead, that outperformance can be attributed to a consistently lower reconstitution drag. Of course, real stock indexes are reconstituted less frequently than monthly and often use rules that take more than just capitalization into account, but the general trend is still in favor of the broader universe. Small-cap stock indexes possess the additional advantage of having a reconstitution boost, as stocks that ascend out of the universe are sold at a profit and replaced with recent losers from the relevant large-cap index.
We can use the same techniques to analyze the reconstitution drag on portfolios of stocks selected purely by their volatility. We now consider the universe of the top 3,000 stocks. (There’s no reason we couldn’t stay with the top 1,000, but the effect we wish to analyze is stronger within the broader universe of stocks.) Volatility for any stock in the universe is estimated by analyzing the standard deviation of its daily returns (including dividends) for the previous year. Each of the following strategies is reconstituted monthly and is cap weighted:
• Portfolio “LoVol” invests in the lowest 20 percent of the eligible names by volatility.
• Portfolio “HiVol” invests in the highest 20 percent of the eligible names by volatility.
• The index invests in all of the eligible names, cap-weighted.
Over the period from January 1974 through November 2011, LoVol beats the index by 59 basis points a year on a compound basis. Also, as predicted, the reconstitution drag on LoVol is indeed less than that of the index — by 57 basis points. As for HiVol, its performance relative to the index is truly dismal: It underperforms by 592 basis points a year on a compound basis. Again, as expected, the reconstitution drag on HiVol is greater than that for the index; the difference turns out to be a whopping 823 basis points a year, even though the total portfolio weight that contributes to it is typically about 1 to 5 percent per month. This 823-basis-point drag is greater than the 592-basis-point annual average underperformance, suggesting that the high-volatility stocks may actually have higher returns than the average stock on an individual basis. Unfortunately, the drag on performance associated with the trading required to stay true to style is so great that it overwhelms any such stock-level advantage.
In short, the low-volatility anomaly isn’t really an anomaly at all. Instead, this effect is a predictable consequence of the relationship between volatility and rebalancing costs, and it should not be surprising that it is observed in just about every data set available.
What would it take to make the effect disappear? Essentially, low-volatility stocks would have to start experiencing returns much lower than those of high-volatility stocks. This is highly unlikely to happen; after all, a similar arbitraging effect has not occurred with small-cap stocks, even though the small-minus-large size effect has been well known for decades. Moreover, even if a return differential arises in the future, the role of rebalancing will still be relevant.
We have now seen a few examples of the material contribution of rebalancing to the long-term performance of rules-based portfolios. It is certainly true that not all sources of excess return can be usefully understood within this framework. For instance, as noted previously, rebalancing is unlikely to have much of an effect on strategies concentrated on a small collection of stocks that are rarely traded (such as those held by high-conviction fundamental managers).
Nevertheless, many traditional quantitative factors, in addition to size and volatility, are strongly affected by reconstitution or rebalancing effects. Our analysis even calls into question the efficacy of the Fama-French three-factor analysis, which is widely used in portfolio performance attribution. We have already proposed that the observed size effect is in reality a direct consequence of rebalancing. There is good reason to believe that this may also explain at least part of the historical outperformance of the value and momentum factors. A portfolio exposed to any or all of the factors may be deriving most of its return from rebalancing instead of individual stock performance. Certainly, more research is required in this regard.
We believe that the main objective of a low-volatility equity portfolio should be to provide returns that approximate those of a cap-weighted index in the long term while simultaneously reducing volatility as much as possible. This goal is not far-fetched, because the cap-weighted index does not take full advantage of the compounding effect of rebalancing and is therefore unlikely to be mean-variance-efficient.
Reducing portfolio volatility is a desirable objective in and of itself. Lower volatility means more-consistent performance and a greater probability of matching long-term goals in a shorter time. Lower volatility does not automatically imply higher returns across asset classes. For example, a portfolio that invests 50 percent in a stock index and 50 percent in cash will have a lower expected return than a stock index portfolio. Nevertheless, when one stays within the realm of fully invested equity portfolios, it appears that most legitimate efforts to lower portfolio volatility actually increase long-term returns. This is not as surprising when placed in the context of the above discussion. Systematically lowering portfolio volatility results in adopting methodologies that are likely to reduce the reconstitution drag or increase the portfolio excess growth.
Investors can enjoy the best of both worlds: reduced volatility without lower return. Low-volatility equity portfolios offer a credible promise of long-term improvements in efficiency, exhibiting higher Sharpe ratios that are likely to persist independently of the existence of a high-volatility premium.
It is possible to achieve even higher Sharpe ratios by adopting a dynamic approach. Attempting to reduce volatility over a cap-weighted index by a constant factor of 20 percent, while preserving the average return, does produce a higher Sharpe ratio than the market. However, attempting to reduce volatility more when the index volatility is higher should exhibit an even higher Sharpe ratio while simultaneously providing more protection when it is most needed.
The above perspectives highlight the following pros and cons of some of the available categories of offerings in the low-volatility equity space:
Portfolios of low-volatility stocks. These are normally branded as low-volatility or defensive-style indexes. As such, they often have low-to-medium fees, are relatively transparently constructed and may well be more efficient than cap-weighted portfolios. However, their efficiency is unlikely to be optimal because of lack of control on both the risk and the reward sides.
Minimum-variance portfolios. These strategies should in principle profit from both rebalancing and optimization, and target portfolio volatility explicitly. Their fees are often low-to-medium as well. The methodology is not transparent: Even the indexlike offerings in this category usually depend on proprietary covariance estimation methodologies. Unconstrained minimization of variance tends to result in a huge turnover, so realistic implementations rely on stringent turnover controls, which may result in higher volatility than anticipated.
Active low-volatility portfolios. This class of strategies includes methodologies with an explicit alpha-generation mechanism independent of simply reducing volatility at the stock or portfolio level. Returns may be increased by traditional stock selection, fundamental overlays or quantitative factors. Because both risk and reward are carefully considered, portfolio efficiency may well be higher than in both of the above options. On the other hand, fees and turnover may be somewhat higher.
Regardless of the approach, low-volatility equity portfolios provide a way to gain efficiency over cap-weighted indexes. Understanding the construction and behavior of such strategies is significant for investors because volatility reduction allows greater allocation to equities at the same level of risk contribution. Rules-based approaches that reduce volatility will generally lead to more-efficient rebalancing. The efficiency can be further increased by targeting the portfolio-level rebalancing effect in a systematic manner. The nature and persistence of the low-volatility anomaly should not distract from the potential for low-volatility equity portfolios to be an extremely valuable component of an institutional investor’s overall portfolio. • •
Adrian Banner is CIO of INTECH Investment Management, a West Palm Beach, Florida–based global institutional investment manager with $40 billion in assets. Banner works in INTECH’s research office in Princeton, New Jersey, alongside director of research Vassilios Papathanakos and associate director of research Phillip Whitman. INTECH uses a mathematical and scientific approach to managing equity portfolios and is an independently managed subsidiary of Denver-based Janus Capital Group.






